Short GRBS
In Ghirlanda et al. 2016 a fitting algorithm was used to determine the redshift and luminosity of short GRBS. We can use the parameters to reproduce the population and the observed GBM survey.
[1]:
from popsynth import SFRDistribution, BPLDistribution, PopulationSynth, NormalAuxSampler, AuxiliarySampler, HardFluxSelection
from popsynth import update_logging_level
update_logging_level("INFO")
[2]:
%matplotlib inline
import matplotlib.pyplot as plt
from jupyterthemes import jtplot
jtplot.style(context="notebook", fscale=1, grid=False)
purple = "#B833FF"
yellow = "#F6EF5B"
import networkx as nx
import numpy as np
import warnings
warnings.simplefilter("ignore")
In the work, the luminosity function of short GRBs is model as a broken power law.
[3]:
bpl = BPLDistribution()
bpl.alpha = -0.53
bpl.beta = -3.4
bpl.Lmin = 1e47 # erg/s
bpl.Lbreak = 2.8e52
bpl.Lmax = 1e55
To model the redshift distribution, an empirical form from Cole et al 2001 is used. In popsynth we call this the SFRDistribution (but perhaps a better name is needed).
[4]:
sfr = SFRDistribution()
[5]:
sfr.r0 = 5.
sfr.a = 1
sfr.rise = 2.8
sfr.decay = 3.5
sfr.peak = 2.3
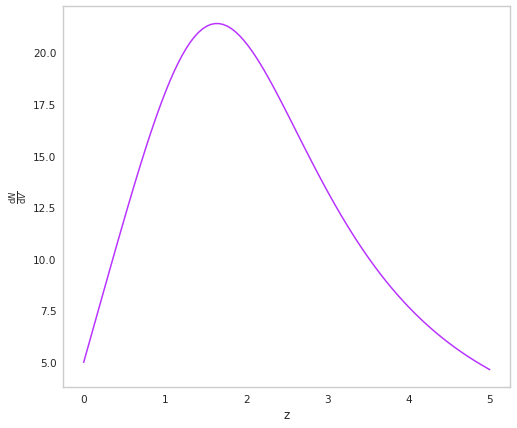
We can checkout how the rate changes with redshift
[6]:
fig, ax = plt.subplots()
z = np.linspace(0,5,100)
ax.plot(z, sfr.dNdV(z), color=purple)
ax.set_xlabel("z")
ax.set_ylabel(r"$\frac{\mathrm{d}N}{\mathrm{d}V}$")
[6]:
Text(0, 0.5, '$\\frac{\\mathrm{d}N}{\\mathrm{d}V}$')
In their model, the authors also have some secondary parameters that are connected to the luminosity. These are the parameters for the spectrum of the GRB. It is proposed that the spectra peak energy (Ep) is linked to the luminosity by a power law relation:
We can build an auxiliary sample to simulate this as well. But we will also add a bit of scatter to the intercept of the relation.
[7]:
intercept =NormalAuxSampler(name="intercept", observed=False)
intercept.mu = 0.034
intercept.sigma = .005
[8]:
class EpSampler(AuxiliarySampler):
_auxiliary_sampler_name = "EpSampler"
def __init__(self):
# pass up to the super class
super(EpSampler, self).__init__("Ep", observed=True, uses_luminosity = True)
def true_sampler(self, size):
# we will get the intercept's latent (true) value
# from its sampler
intercept = self._secondary_samplers["intercept"].true_values
slope = 0.84
self._true_values = np.power(10., intercept + slope * np.log10(self._luminosity/1e52) + np.log10(670.))
def observation_sampler(self, size):
# we will also add some measurement error to Ep
self._obs_values = self._true_values + np.random.normal(0., 10, size=size)
Now we can put it all together.
[9]:
pop_synth = PopulationSynth(spatial_distribution=sfr, luminosity_distribution=bpl)
We will have a hard flux selection which is Fermi-GBM’s fluz limit of ~ 1e-7 erg/s/cm2
[10]:
selection = HardFluxSelection()
selection.boundary = 1e-7
[11]:
pop_synth.set_flux_selection(selection)
We need to add the Ep sampler. Once we set the intercept sampler as a secondary it will automatically be added to the population synth.
[12]:
ep = EpSampler()
[13]:
ep.set_secondary_sampler(intercept)
[14]:
pop_synth.add_auxiliary_sampler(ep)
INFO | registering auxilary sampler: Ep
We are ready to sample our population. We will add some measurement uncertainty to the fluxes as well.
[15]:
population = pop_synth.draw_survey(flux_sigma=0.2)
INFO | The volume integral is 797.5506658438255
INFO | Expecting 770 total objects
INFO | Sampling: Ep
INFO | Ep is sampling its secondary quantities
INFO | Sampling: intercept
INFO | applying selection to fluxes
INFO | Detected 499 distances
INFO | Detected 499 objects out to a distance of 5.31
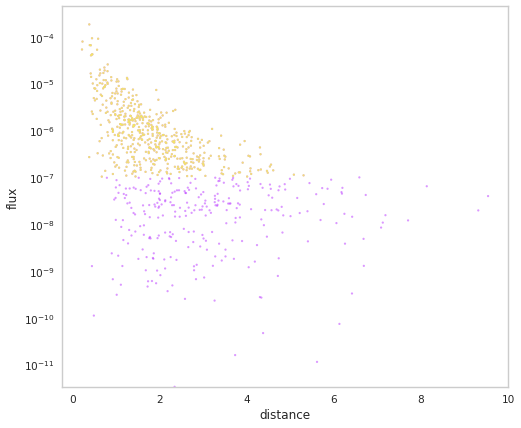
[16]:
population.display_fluxes(true_color=purple, obs_color=yellow, with_arrows=False, s= 5);
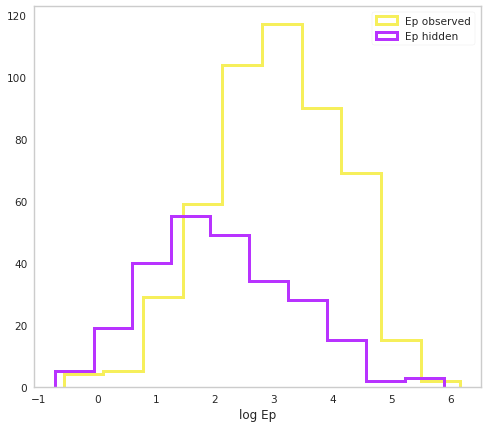
Let’s look at our distribution of Ep
[17]:
fig, ax = plt.subplots()
ax.hist(np.log10(population.Ep.selected), histtype="step", color=yellow, lw=3, label="Ep observed")
ax.hist(np.log10(population.Ep.non_selected), histtype="step", color=purple, lw=3, label="Ep hidden")
ax.set_xlabel("log Ep")
ax.legend()
[17]:
<matplotlib.legend.Legend at 0x7f14b9a12190>
[18]:
fig, ax = plt.subplots()
ax.scatter(population.fluxes.non_selected,
population.Ep.non_selected,c=purple, alpha=0.5)
ax.scatter(population.fluxes.selected,
population.Ep.selected,c=yellow, alpha=0.5)
ax.set_xscale("log")
ax.set_yscale("log")
ax.set_xlabel("log Ep")
ax.set_xlabel("log Flux")
[18]:
Text(0.5, 0, 'log Flux')
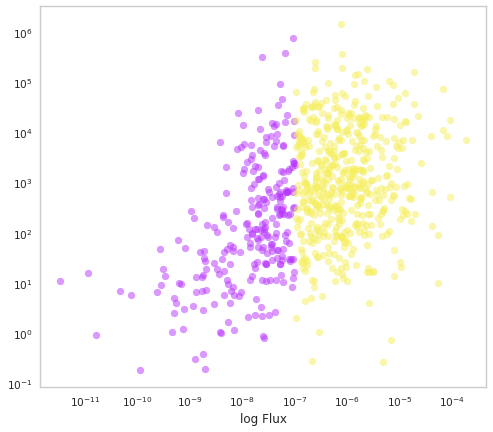
Does this look like the observed catalogs?